A Measurement Error Model of Dichotomous Democracy Status
03 Feb 2016I’m not actually a political scientist, but I like to pretend I am sometimes. Jay Ulfelder and I just submitted a draft of our paper to SSRN that you can check out. Here’s the abstract:
We use a Bayesian measurement error model to derive a probabilistic measure of democracy from several existing dichotomous data sets. This approach accepts the premise that democracy may usefully be construed as a bivalent concept for certain theoretical and technical purposes, but it also makes more explicit our collective uncertainty about where some cases fall in that binary scheme. We believe the resulting data provide a firmer foundation than measures of countries’ degree of democracy for studies that require a dichotomous measure of regime type.
This allows us to do things like, measure the probabilistic concept like “an expert would say a country in a region is democratic,” borrowing information across time to produce plots like this one:
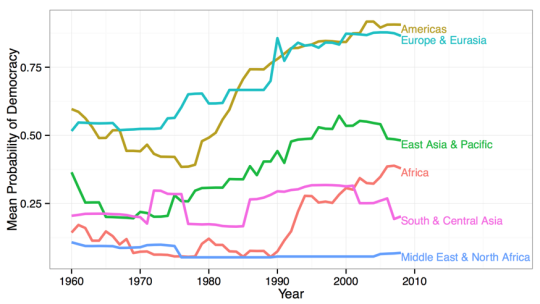
##
How we did it
This research is totally open and reproducible. We used R and Python as well as some Stan to to implement our HMC estimation. The code and the source data are available on github.
How this came about
I met Jay Ulfelder on Twitter a couple years ago and we periodically discuss research over email. He emailed me last year to ask:
Is there a statistical model or process you know that solves the following problem?
Say you have 2 to 5 more or less independent, binary measures of the same thing in a time-series cross-sectional data set. Let’s call those measures “votes” and think of them as each sources’ best guess at the yes/no status of each record on some feature of interest. Is there a way—probably some kind of Bayesian model that didn’t even exist when I was in grad school—to use those votes to generate a unified probabilistic measure or z-score or something similar of each case’s status?
I had an idea about how to do this right away: item-response models provide a nice framework for thinking about this and all we had to do was model the underlying time series process. Bayesian inference was a perfect fit for this problem.